Что такое ссылочное ранжирование (PageRank)
Как уже говорилось выше, поисковые машины анализируют структуру ссылок веб-страниц друг на друга. Таким образом выясняется авторитет отдельных страниц (и сайтов в целом) среди сетевого сообщества, среди тех, кто создает сайты и делает на них ссылки на другие сайты.
Сама по себе эта идея не нова — она представляет собой автоматизированный вариант довольно старой идеи индекса цитируемости, который используется в научном мире для вычисления авторитета ученого. Идея проста — кого больше цитируют и на кого чаще ссылаются, тот авторитетен, а его работы, очевидно, больше нужны человечеству. Тот же, кого цитируют меньше, человечеству менее интересен.
Поэтому к обычной «текстовой релевантности», основанной на соответствии самого текста страницы запросу, можно добавить «авторитетность» страницы среди других страниц.
Впервые эту идею применили в публичной поисковой машине в конце 1990-х годов создатели Google — Брин и Пейдж, аспиранты Стэнфордского университета. Для них, конечно, идея научного индекса цитирования была естественной и давно известной.
Именно ссылочный ранг страницы стал основным принципом ранжирования результатов поиска в Google, что привело к резкому отрыву от конкурентов по качеству поиска и стало одной из основных причин доминирования Google в мировом Интернете. Они назвали этот ссылочный ранг PageRank (ранг страницы), включив заодно в название также и фамилию одного из двух авторов идеи — Ларри Пейджа (Larry Page).
КАК ВЫЧИСЛЯЕТСЯ РАНГ СТРАНИЦЫ
Теоретически идея автоматического использования ссылок для вычисления авторитета страницы выглядит просто: возьмем матрицу всех ссылок всех страниц Интернета друг на друга, то есть фактически «Интернет в квадрате». Получится матрица гигантских размеров — скажем, двадцать миллиардов на двадцать миллиардов.
Теперь начнем учитывать ссылки страниц друг на друга. Сначала присвоим всем страницам равный вес (ранг). Затем, начиная с какого-нибудь угла этой огромной матрицы, начнем пересчитывать вес страниц и ссылок примерно таким образом: если на страницу ссылается много страниц (т. е. у нее много «входящих» ссылок), то ее ранг повышается (по некоторой относительно простой формуле).
Будем также учитывать и ранг ссылок. Ведь ссылка с важной страницы лучше ссылки с малозначимой страницы, не так ли? Если на вас сослался президент в своей ежегодной речи, то это более ценно, чем если вас вчера упомянул во дворе дворник.
Итак, при расчете ранга страницы нужно учесть вес каждой «входящей» ссылки.
Наоборот, если со страницы с неким рангом «уходит» несколько ссылок, разделим ранг страницы между всеми ссылками. Действительно, если президент в своей речи сослался исключительно на вас одного — это серьезное событие. Если же он зачитал список из двухсот имен, среди которых было и ваше, то это тоже почетно, но в меньшей степени.
Таким образом, если на страницу ссылается очень авторитетный ресурс, то и ранг самой страницы повышается. Правда, если этот авторитетный ресурс ссылается еще на тысячи других страниц (скажем, каталог Yahoo!), то авторитет каталога «размажется» по всем тысячам ссылок и нам от него достанется немного (другими словами, ранг нашей страницы повысится незначительно).
Заметим, что, завершив первый цикл пересчета матрицы связей Интернета, нам придется вернуться к началу и пересчитать все ранги еще раз, так как ранги страниц, ссылающихся на самые первые страницы (с которых мы начинали), уже изменились. И таких повторений пересчета (так называемых итераций) придется сделать много.
В ходе разработки алгоритма создателям Google пришлось доказать эргодическую теорему о том, что процесс пересчета матрицы сойдется, как говорят математики. Получается, что на самом деле достаточно пересчитать матрицу всего несколько раз, чтобы ранги страниц уже были более-менее стабильны и ими можно было пользоваться в поисковике для расчета релевантности.
Математический рейтинг вебстраницы (PageRank) для простой сети, выраженный в процентах.
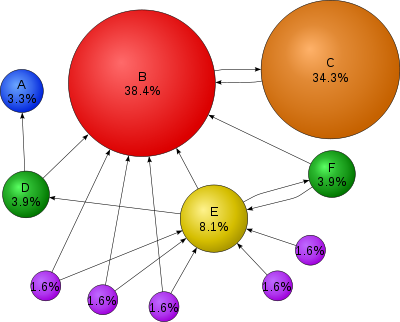
Вебстраница C имеет более высокий рейтинг, чем страница E, хотя есть меньше ссылок на C чем на Е, но одна из ссылок на C исходит из более важных страниц и, следовательно, имеет более высокое значение. Если условно считать что веб-пользователь который находится на случайной странице имеет 85 % вероятность выбора случайной ссылки, и 15 % оставления этой страницы без всякого перехода на её ссылки, то вероятности перехода к странице E с других ссылок равна 8,1 % времени. (15 % вероятности перехода к произвольной странице соответствует коэффициенту затухания 85 %.) Без затухания, все веб-пользователи в конечном итоге попадают на страницы A, B или С, и все остальные страницы будет иметь PageRank нуля. При наличии затухания, страница А эффективно связывает почти все ссылки на страницы в этой Сети, даже если она не имеет своих собственных исходящих ссылок.
Для расчета авторитетности сайта нужно пересчитывать гигантские таблицы ссылок с длиной, равной количеству всех страниц в Интернете. Технически задача такого пересчета гигантских матриц очень сложна. Именно поэтому даже спустя шесть-семь лет после запуска Google пересчитывает свой индекс не так уж часто, поскольку для пересчета матрицы связей требуются огромные вычислительные мощности.
Зато и выигрыш в релевантности поиска в Google был значительным. Сейчас, спустя много лет, все поисковые машины (в том числе «Яндекс» и «Рамблер») применяют расчет авторитетности страницы и ссылочный ранг в том или ином виде для вычисления релевантности результатов поиска.
Со временем идея вычисления авторитетности страницы была усовершенствована за счет учета текста на ссылках. Действительно, почти каждая ссылка в Интернете представляет собой какой-то текст (под него и «подложен», собственно, адрес страницы, на которую ссылаются). Естественно учитывать этот текст при расчете ранга той страницы, на которую ведет ссылка. Так возникает ссылочный ранг страницы — ранг, учитывающий тему ссылок.
Пример
ССЫЛОЧНЫЙ РАНГ СТРАНИЦЫ
Допустим, автор сайта написал у себя на сайте фразу «хорошие стрелялки и мочилки для мобильников» и дал под ней ссылку на некоторую страницу X, рассказывающую об играх для мобильных телефонов. Ясно, что эти слова нужно как минимум добавить к индексу этой страницы X, даже если на ней самой этих слов нет и если она рассказывает о мобильных играх в более «академическом» стиле.
А если ссылку на страницу Х со словом «стрелялки» дали многие веб-мастера, то и вес слова «стрелялки» для страницы X надо существенно повысить (хотя его вообще нет на странице X).
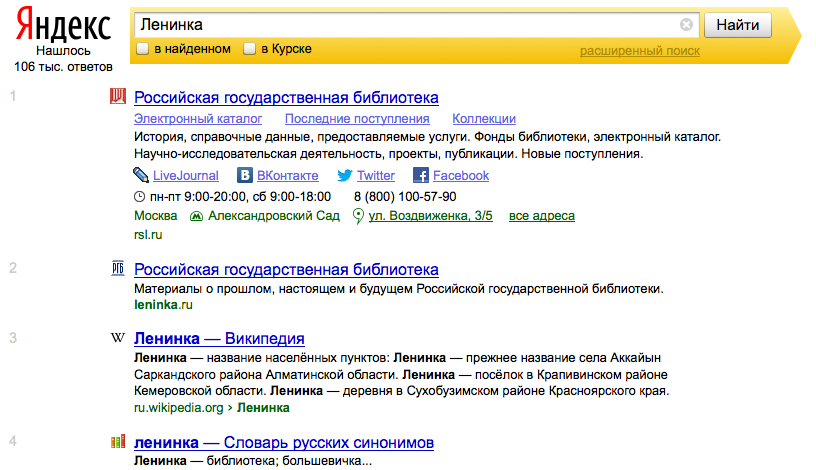
Так, Яндекс как пример приводит сайт Российской Государственной Библиотеки имени В.И. Ленина, который находится и стоит на первой строчке в выдаче при запросе слова «ленинка», несмотря на то, что данное слово в контенте главной страницы не фигурирует. Все дело в том, что система Яндекса выявляет конкретный веб-ресурс по ссылкам со сторонних сайтов. По такой же схеме происходит и поиск иных площадок, станицы которых с механической точки зрения не являются релевантными относительно поисковых запросов, но при этом выступают релевантными по контексту.
| Ранжирование | Ссылочное ранжирование на современном рынке |