Энтропия и информация

Поучительность только что рассмотренного примера в том, что из него отчетливо видно как предшествующий опыт (%%α%%) может уменьшить количество исходов и, следовательно, неопределенность последующего опыта (%%β%%). Разность %%H(β)%% и %%Н_α(β)%%, очевидно, показывает, какие новые сведения относительно %%β%% получаем, произведя опыт %%α%%. Эта величина называется информацией относительно опыта %%β%%, содержащейся в опыте %%α%%.

$$I(α,β) = Н_α(β)~~~(2.13)$$

Данное выражение открывает возможность численного измерения количества информации, поскольку оценивать энтропию уже умеем. Из него легко получить ряд следствий:

Следствие 1. Поскольку единицей измерения энтропии является бит, то в этих же единицах может быть измерено количество информации.

Следствие 2. Пусть опыт %%α = β%%, т.е. просто произведен опыт %%β%%. Поскольку он несет полную информацию о себе самом, неопределенность его исхода полностью снимается, т.е. %%Н_β(β) = 0%%. Тогда %%I(β, β) = Н(β)%%, т.е. можно считать, что

энтропия равна информации относительно опыта, которая содержится в нем самом.

Можно построить уточнение:

энтропия опыта равна той информации, которую получаем в результате его осуществления.

Отметим ряд свойств информации:

1. %%I(α, β) ≥ 0%%, причем %%I(α, β) = 0%% тогда и только тогда, когда опыты %%α%% и %%β%% независимы. Это свойство непосредственно вытекает из (2.10) и (2.13).
2. %%I(α, β) = I(β, α)%%, т.е. информация симметрична относительно последовательности опытов.
3. Следствие 2 и представление энтропии в виде (2.4) позволяют записать:

$$I=-\sum^{n}_{i=1}{p(A_i)\cdot log_2 p(A_i)} ~~~(2.14)$$

т.е. информация опыта равна среднему значению количества информации, содержащейся в каком-либо одном его исходе.

Рассмотрим ряд примеров применения формулы (2.14).

Пример. Какое количество информации требуется, чтобы узнать исход броска монеты? В данном случае %%n = 2%% и события равновероятны, т.е. %%p_1 = р_2 = 0,5%%. Согласно (2.14): $$I = - 0,5 \cdot log_2 0,5 - 0,5 \cdot log_2 0,5 = 1\; бит.$$

Пример: игра «Угадай-ка—4». Некто задумал целое число в интервале от 0 до 3. Наш опыт состоит в угадывании этого числа. На наши вопросы Некто может отвечать лишь «Да» или «Нет». Какое количество информации должны получить, чтобы узнать задуманное число, т.е. полностью снять начальную неопределенность? Как правильно построить процесс угадывания?

Исходами в данном случае являются: %%A_1%% - «задуман 0», %%A_2%% - «задумана 1», %%A_3%% - «задумана 2», %%A_4%% - «задумана 3». Конечно, предполагается, что вероятности быть задуманными у всех чисел одинаковы. Поскольку %%n = 4%%, следовательно,

$$p(A_i) = \frac{1}{4}%%, %%log_2 р(А_i) = -2$$

и %%I = 2%% бит. Таким образом, для полного снятия неопределенности опыта (угадывания задуманного числа) нам необходимо 2 бит информации.

Теперь выясним, какие вопросы необходимо задать, чтобы процесс угадывания был оптимальным, т.е. содержал минимальное их число. Здесь удобно воспользоваться так называемым выборочным каскадом:

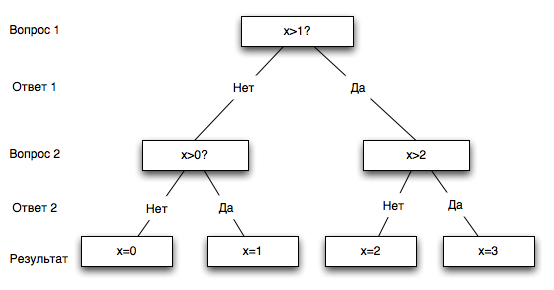
Таким образом, для решения задачи оказалось достаточно 2-х вопросов независимо от того, какое число было задумано. Совпадение между количеством информации и числом вопросов с бинарными ответами неслучайно.

Количество информации численно равно числу вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи. 

В рассмотренном примере два полученных ответа в выборочном каскаде полностью сняли начальную неопределенность. Подобная процедура позволяет определить количество информации в любой задаче, интерпретация которой может быть сведена к парному выбору. Например, определение символа некоторого алфавита, использованного для представления сообщения. Приведенное утверждение перестает быть справедливым в том случае, если каждый из двух возможных ответов имеет разную вероятность – такая ситуация будет рассмотрена позднее.

Легко получить следствие формулы (2.14) для случая, когда все п исходов равновероятны (собственно, именно такие и рассматривались в примерах 2.4 и 2.5). В этом случае все

$$p(A_i) = \frac{1}{n}$$

и, следовательно, $$I=\sum^{n}_{i=1}{\frac{1}{n}\cdot log_2n}=log_2n$$ $$I=log_2n~~~(2.15)$$

Эта формула была выведена в 1928 г. американским инженером Р. Хартли и носит его имя. Она связывает количество равновероятных состояний (n) и количество информации в сообщении (I), что любое из этих состояний реализовалось. Ее смысл в том, что, если некоторое множество содержит n элементов и х принадлежит данному множеству, то для его выделения (однозначной идентификации) среди прочих требуется количество информации, равное %%log_2 n%%.

Частным случаем применения формулы (2.15) является ситуация, когда %%n = 2^k%%; подставляя это значение в (2.15), очевидно, получим:

$$I=k\; бит~~~(2.16)$$

Именно эта ситуация реализовалась в примерах, рассмотренных выше. Анализируя результаты решения, можно прийти к выводу, что k как раз равно количеству вопросов с бинарными равновероятными ответами, которые определяли количество информации в задачах.

Пример. Случайным образом вынимается карта из колоды в 32 карты. Какое количество информации требуется, чтобы угадать, что это за карта? Как построить угадывание? Для данной ситуации %%n = 2^5%%, значит, k = 5 и, следовательно, I = 5 бит. Последовательность вопросов придумайте самостоятельно.

Пример. В некоторой местности имеются две близкорасположенные деревни: %%А%% и %%В%%. Известно, что жители А всегда говорят правду, а жители %%В%% - всегда лгут.

Известно также, что жители обеих деревень любят ходить друг к другу в гости, поэтому в каждой из деревень можно встретить жителя соседней деревни. Путешественник, сбившись ночью с пути оказался в одной из двух деревень и, заговорив с первым встречным, захотел выяснить, в какой деревне он находится и откуда его собеседник. Какое минимальное количество вопросов с бинарными ответами требуется задать путешественнику?

Количество возможных комбинаций, очевидно, равно 4 (путешественник в %%А%%, собеседник из %%А%%; путешественник в %%А%%, собеседник из %%В%%; и т.д.), т.е. %%n = 22%% и, следовательно значит, %%k = 2%%. Последовательность вопросов придумайте самостоятельно.

Попытаемся понять смысл полученных в данном разделе результатов. Необходимо выделить ряд моментов.

1. Выражение (2.14) является статистическим определением понятия «информация», поскольку в него входят вероятности возможных исходов опыта. По сути дается операционное определение новой величины, т.е. устанавливается процедура (способ) измерения величины. Как отмечалось ранее, в науке (научном знании) именно такой метод введения новых терминов считается предпочтительным, поскольку то, что не может быть измерено, не может быть проверено и, следовательно, заслуживает меньшего доверия.

Выражение (2.13) можно интерпретировать следующим образом: если начальная энтропия опыта %%Н_1%%, а в результате сообщения информации %%I%% энтропия становится равной %%Н_2%% (очевидно, %%Н_1 ≥ Н_2%%), то %%I=H_1-H_2%%

т.е. информация равна убыли энтропии. В частном случае, если изначально равновероятных исходов было %%n_1%%, а в результате передачи информации %%I%% неопределенность уменьшилась, и число исходов стало %%n_2%% (очевидно, %%n_2 ≤ n_1%%), то из (2.15) легко получить:

$$I=log_2n_1-log_2n_2=log_2 \frac{n_1}{n_2}$$

Таким образом, можно дать следующее определение:

Информация - это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом; убыль связанной с ним энтропии является количественной мерой информации. В случае равновероятных исходов информация равна логарифму отношения числа возможных исходов до и после (получения сообщения).

2. Как уже было сказано, в статистической механике энтропия характеризует неопределенность, связанную с недостатком информации о состоянии системы. Наибольшей оказывается энтропия у равновесной полностью беспорядочной системы - о ее состоянии наша осведомленность минимальна. Упорядочение системы (наведение какого-то порядка) связано с получением некоторой дополнительной информации и уменьшением энтропии. В теории информации энтропия также отражает неопределенность, однако, это неопределенность иного рода - она связана с незнанием результата опыта с набором случайных возможных исходов. Таким образом, хотя между энтропией в физике и информатике много общего, необходимо сознавать и различие этих понятий. Совершенно очевидно, что в дальнейшем понятие энтропии будет использоваться в аспекте теории информации.

3. Следствием аддитивности энтропии независимых опытов (2.5) оказывается аддитивность информации. Пусть с выбором одного из элементов (%%х_A%%) множества %%А%%, содержащего %%n_A%% элементов, связано %%I_А = log_2 n_A%% информации, а с выбором %%х_B%% из %%В%% с %%n_B%% элементами информации связано %%I_B = log_2 n_B%% и второй выбор никак не связан с первым, то при объединении множеств число возможных состояний (элементов) будет %%n = n_А \cdot n_B%% и для выбора комбинации %%х_Aх_B%% потребуется количество информации:

%%I=log_2n_A\cdot log_2 n_B = log_2n_A + log_2 n_B = I_A+I_B%%

4. Вернемся к утверждению о том, что количество информации может быть измерено числом вопросов с двумя равновероятными ответами. Означает ли это, что %%I%% должна быть всегда величиной целой? Из формулы Хартли (2.15), как было показано, %%I = k%% бит (т.е. целому числу бит) только в случае %%n = 2k%%. А в остальных ситуациях?

Например, при игре «Угадай-ка - 7» (угадать число от 0 до 6) нужно в выборочном каскаде задать %%n ≥ log_2 7 = 2,807%%, т.е. необходимо задать три вопроса, поскольку количество вопросов - это целое число.

Однако представим, что одновременно играем в шесть таких же игр. Тогда необходимо отгадать одну из возможных комбинаций, которых всего

%%N=n_1n_2...n_7=7^6=117649<2^{17}=131072%%

Следовательно, для угадывания всей шестизначной комбинации требуется %%I = 17%% бит информации, т.е. нужно задать 17 вопросов. В среднем на один элемент (одну игру) приходится %%\frac{17}{3} = 2,833%% вопроса, что близко к значению %%log_2 7%%. Таким образом,

величина %%I%%, определяемая описанным выше образом, показывает, сколько в среднем необходимо сделать парных выборов для установления результата (полного снятия неопределенности), если опыт повторить многократно %%(n →\infty )%%.

5. Необходимо понимать также, что не всегда с каждым из ответов на вопрос, имеющий только с два варианта ответа (будем далее называть такие вопросы бинарными), связан ровно 1 бит информации. Рассмотрим опыт, реализующийся посредством двух случайных событий; поскольку их всего два, очевидно, они являются дополнительными друг другу. Если эти события равновероятны, %%р_1 = р_2 = \frac{1}{2}%%, и %%I = 1%% бит, как следует из формулы Хартли и (2.14). Однако, если их вероятности различны: %%р_1 = р%%, то

%%p_2 = 1 - р%%, и из (2.14) получаем функцию:

$$I(p)=-p log_2p-(1-p)\cdot log_2(1-p)$$

Легко показать, что при %%р → 0%% и при %%р → 1%% функция %%I(р) → 0%%. Ситуация может быть проиллюстрирована графиком, из которого, в частности, видно, что кривая симметрична относительно р = 0,5 и достигает максимума при этом значении. Если теперь считать, что событие 1 - это утвердительный ответ на бинарный вопрос, а событие 2 - отрицательный, то приходим к заключению:

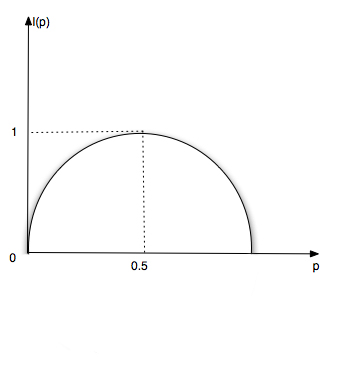
Ответ на бинарный вопрос может содержать не более 1 бит информации; информация равна 1 бит только для равновероятных ответов; в остальных случаях она меньше 1 бит.

Пример. При угадывании результата броска игральной кости задается вопрос «Выпало 6?». Какое количество информации содержит ответ?

%%р= \frac{1}{6}%%, %%1 - р = \frac{5}{6}%%, следовательно, из (2.14) $$I(р) = \frac{1}{6} \cdot log_2 6 + \frac{5}{6} \cdot log_2 1.2 = 0,65\; бит < 1\; бит.$$

6. Формула (2.14) приводит еще к одному выводу. Пусть некоторый опыт имеет два исхода А и В, причем %%р_А = 0,99%% , а %%р_B = 0,01%%. В случае исхода А получим количество информации %%I_А = - log_2 0,99 = 0,0145\; бит%%. В случае исхода B количество информации оказывается равным %%I_В = - log_2 0,01 = 6,644\; бит%%. Другими словами, больше информации связано с теми исходами, которые менее вероятны. Действительно, то, что наступит именно А, почти наверняка знали и до опыта; поэтому реализация такого исхода очень мало добавляет к нашей осведомленности. Наоборот, исход В - весьма редкий; информации с ним связано больше (осуществилось трудно ожидаемое событие). Однако такое большое количество информации будем при повторах опыта получать редко, поскольку мала вероятность В. Среднее же количество информации согласно (2.14) равно

$$I = 0,99 \cdot I_А + 0,01 \cdot I_В ≈ 0,081\; бит$$

7. Нами рассмотрен вероятностный подход к определению количества информации. Он не является единственным. Как будет показано далее, количество информации можно связать с числом знаков в дискретном сообщении - такой способ измерения называется объемным. Можно доказать, что при любом варианте кодирования информации %%I_{вер}< I_{об}%%.

8. Объективность информации. При использовании людьми одна и та же информация может иметь различную оценку с точки зрения значимости (важности, ценности). Определяющим в такой оценке оказывается содержание (смысл) сообщения для конкретного потребителя. Однако при решении практических задач технического характера содержание сообщения может не играть роли. Например, задача телеграфной (и любой другой) линии связи является точная и безошибочная передача сообщения без анализа того, насколько ценной для получателя оказывается связанная с ним информация. Техническое устройство не может оценить важности информации - его задача без потерь передать или сохранить информацию. Выше определили информацию как результат выбора. Такое определение не зависит от того, кто и каким образом осуществляет выбор, а связанная с ним количественная мера информации - одинаковой для любого потребителя.

Следовательно, появляется возможность объективного измерения информации, при этом результат измерения - абсолютен. Это служит предпосылкой для решения технических задач. Нельзя предложить абсолютной и единой для всех меры ценности информации. С точки зрения формальной информации страница из учебника информатики или из романа «Война и мир» и страница, записанная бессмысленными значками, содержат одинаковое количество информации. Количественная сторона информации объективна, смысловая - нет. Однако, жертвуя смысловой (семантической) стороной информации, получаем объективные методы измерения ее количества, а также обретаем возможность описывать информационные процессы математическими уравнениями. Это является приближением и в то же время условием применимости законов теории информации к анализу и описанию информационных процессов.

9. Информация и знание. На бытовом уровне, в науках социальной направленности, например в педагогике «информация» отождествляется с «информированностью», т.е. человеческим знанием, которое, в свою очередь, связано с оценкой смысла информации. В теории информации же, напротив, информация является мерой нашего незнания чего-либо (но что в принципе может произойти); как только это происходит и узнаем результат, информация, связанная с данным событием, исчезает. Состоявшееся событие не несет информации, поскольку пропадает его неопределенность (энтропия становится равной нулю), и согласно (2.13) %%I = 0%%.

Последние два замечания представляются весьма важными, поскольку недопонимание указанных в них обстоятельств порождает попытки применения законов теории информации в тех сферах, где условия ее применимости не выполнены. Это, в свою очередь, порождает отрицательные результаты, которые служат причиной разочарования в самой теории. Однако любая теория, в том числе и теория информации, справедлива лишь в рамках своих исходных ограничений.