Решение типовых примеров
Пример 1
Опыт состоит в однократном бросании игральной кости. Опишем пространство элементарных исходов %%\Omega%% и укажем состав подмножеств, соответствующих следующим событиям:
- %%A%% — число очков, выпавших на верхней грани игральной кости, кратно четырем;
- %%B%% — на верхней грани игральной кости выпало четное число очков;
- %%C%% — число очков, выпавших на верхней грани меньше четырех;
- %%D%% — число очков, выпавших на верхней грани меньше или равно %%6%%;
Установим пары совместных событий.
Решение
Пространство элементарных исходов в данном опыте имеет вид $$ \Omega = \{\omega_1, \omega_2, \omega_3, \omega_4, \omega_5, \omega_6\}, $$ где %%\omega_i%% — выпадение на верхней грани игральной кости %%i%% очков.
- Событие %%A%% происходит тогда и только тогда, когда выпадает %%4%%, т.е. %%A = \{\omega_4\}%%.
Событие %%B%% происходит тогда и только тогда, когда выпадает %%2%%, %%4%%, %%6%% очков, т.е. %%B = \{\omega_2, \omega_4, \omega_6\}%%.
Аналогично получаем следующие выражения для описанных событий.
- %%C = \{\omega_1, \omega_2, \omega_3\}%%.
- %%D = \{\omega_1, \omega_2, \omega_3, \omega_4, \omega_5, \omega_6\} = \Omega%%.
Сопоставляя попарно события и проверяя наличие общих элементов, находим пары совместных событий: %%A%% и %%B%%, %%A%% и %%D%%, %%B%% и %%C%%, %%B%% и %%D%%, %%C%% и %%D%%.
Пример 2
Игральную кость бросают один раз. События %%A%%, %%B%%, %%C%%, %%D%% определены в примере 1. Опишем следющие события:
- %%E = \overline{C}%%;
- %%F = AB%%;
- %%G = B \cup C%%;
- %%H = D B \setminus A%%;
Решение
Событие противоположное событию %%C%% является выпадение числа очков большее или равное %%4%%, т.е. %%E = \{\omega_4, \omega_5, \omega_6\}%%.
Аналогично получаем следующие выражения для описанных событий.
- %%F = \{\omega_4\}%%;
- %%G = \{\omega_1, \omega_2, \omega_3, \omega_4, \omega_6\}%%;
- %%H = \{\omega_1, \omega_2, \omega_3, \omega_5, \omega_6\}%%;
Пример 3
Из множества всех студентов наугад выбирают двух студентов: парня и девушку. Событие %%A%% — парню больше %%21%% года, событие %%B%% — девушка старше парня, событие %%C%% — девушка замужем.
Выясним смысл следующих событий:
- %%ABC%%;
- %%A \setminus BC%%;
- %%B\overline{C}%%.
Решение
- %%ABC%% — Пара, где девушка старше парня и замужем и парню больше %%21%% года.
- %%A \setminus BC%% — пара, где парень старше %%21%%, причем не младше девушки, и девушка не замужем.
- %%B\overline{C}%% — пара, где девушка старше парня и не замужем.
Пример 4
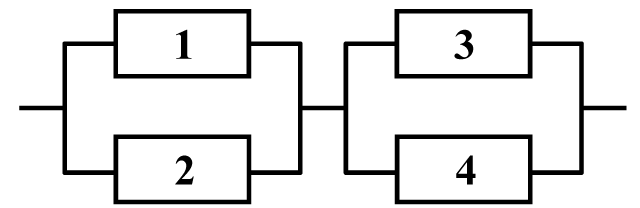
Рис. 1 Схема устройства
Схема устройства электрической цепи приведена на рисунке 1. Выход из строя элемента %%i%% — событие %%A_i, i = \overline{1,4}%%. Запишем выражение события разрыва цепи.
Решение
Обозначим разрыв цепи в качестве события %%A%%. Разрыв цепи произойдет, если выйдут из строя элементы %%1%% и %%2%% или %%3%% и %%4%%, т.е. произойдут события %%A_1 A_2%% или %%A_3 A_4%%. Поэтому $$ A = A_1 A_2 \cup A_3 A_4. $$
| Свойства операций над событиями | Проверка знаний: события |