Кодирование чисел в компьютере и действия над ними

В предыдущем разделе обсуждалась возможность представления чисел в двоичной системе счисления. Результатом этого обсуждения могло бы стать следующее резюме: двоичное представление возможно; имеется однозначное соответствие между двоичным и любым другим (в частности, десятичным) позиционным представлением; представление возможно как в форме с фиксированной, так и в форме с плавающей запятой; имеются алгоритмы преобразования чисел между системами счисления при различных формах их представления.

Как указывалось в ранее, второй важной специфической особенностью представления чисел в регистрах и в памяти компьютера является то, что, в отличие от записи числа на бумаге, компьютерные ячейки имеют ограниченный размер и, следовательно, вынуждают использовать при записи чисел и действиях с ними конечное количество разрядов. Это приводит к тому, что бесконечное множество вещественных чисел заменяется конечным множеством их представлений, которые называются кодами чисел, а обычные арифметические операции с числами заменяются операциями с кодами.

Способы кодирования и допустимые над ними действия оказываются различными для следующих числовых множеств:

• целые положительные числа (целые числа без знака);
• целые числа со знаком;
• вещественные нормализованные числа.

Рассмотрим подробнее перечисленные группы.

Кодирование и обработка в компьютере целых чисел без знака

Будем исходить из того, что для записи числа в устройствах компьютера выделяется фиксированное количество двоичных разрядов. Память компьютера имеет байтовую структуру, однако, размер одной адресуемой ячейки обычно составляет несколько байт. Например, в компьютерах IBM ячейка памяти объединяет 2 байта (16 двоичных разрядов) - такая комбинация связанных соседних ячеек, обрабатываемая совместно, называется машинным словом. Для представления числа в регистре арифметико-логического устройства процессора, где формируется результат операции, имеется еще один дополнительный одноразрядный регистр, который называется регистром переноса и который можно рассматривать в качестве продолжения (т.е. 17-го бита) регистра результата. Назначение этого бита выяснится чуть позже.

Конечный размер разрядной сетки порождает понятие «наибольшее целое число», которого в обычном (немашинном) представлении чисел просто не существует. Если количество разрядов %%k%% и %%p = 2%%, то, согласно (4.8), %%(Z_2)^{max} = 2^k - 1%%. В частности, при %%k = 16%%

$$(Z_2)^{max} = 2^{16} - 1 = 111111111111111_2 = 65535_{10}$$

Другими словами, целого числа, скажем, 65636 и более в компьютере просто не может существовать и, следовательно, появление в ходе вычислений чисел, превышающих %%(Z_2)^{max}%%, должно интерпретироваться как ошибка. Минимальным целым числом в беззнаковом представлении, очевидно, является %%(Z_2)^{min} = 000000000000000_2 = 0_{10}%%.

Longint является типом целого числа со знаком.

В языках программирования целые числа без знака, для записи которых отводится, как правило, 2 байта, определены как некоторый тип данных. Тип устанавливает способ кодирования числа, количество отводимых для записи ячеек памяти (т.е. разрядность числа), а также перечень допустимых операций при обработке. Выход за границу 65535 возможен только путем увеличения количества разрядов для записи числа, но это порождает новый тип со своим %%Z_{max}%%; например, тип longint (Java) с максимальным значением 214748364710, числа которого занимают 4 байта.

Рассмотрим, как с беззнаковыми числами выполняются арифметические операции, не меняющие типа числа; очевидно, к ним относятся сложение и умножение.

Сложение производится согласно таблице сложения, которая для двоичных чисел имеет вид:

0+0=0
1+0=1
0+1=1
1+1=10

В последнем случае в том разряде, где находились слагаемые, оказывается 0, а 1 переносится в старший разряд. Место, где сохраняется переносимая в старший разряд 1 до того, как она будет использована в операции, называется битом переноса.

Пример. Найти сумму %%9876_{10} + 12345_{10}%% при беззнаковой двоичной кодировке и 16-битном машинном слове. После перевода слагаемых в двоичную систему счисления и выполнения сложения получим (для удобства восприятия 16-ти разрядное число разобьем на группы по четыре разряда):

Пример. Найти сумму %%65534_{10} + 3_{10}%%

В последнем примере в результате сложения получилось число, превышающее максимально возможное; результат ошибочен, о чем свидетельствует появление 1 в регистре переполнения. Возникновение такой ситуации в ходе выполнения программы, написанной на языке, где предусмотрено строгое описание типа переменных, приводит к прекращению работы и выводу сообщения об ошибке. В программах, предназначенных для обработки числовой информации (например, Excel, MathCAD или Calc), при переполнении разрядной сетки производится автоматическое преобразование целого числа в вещественный тип. Таким образом, регистр переноса в данном случае служит индикатором корректности процесса вычислений.

Умножение производится согласно таблице умножения, которая для двоичных чисел имеет предельно простой вид:

0x0=0
1x0=0
0x1=0
1x1=1

Пример. Найти произведение %%13_{10} \times 5_{10}%%.Операции выполнить в двоичной системе счисления.

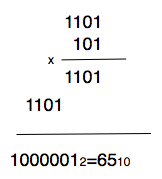
Таким образом, умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0. Сдвиг всегда чередуется со сложением из-за ограниченности числа регистров, которые имеются в процессоре для размещения операндов. Другими словами, реализации отдельной операции умножения в процессоре не требуется.

Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение. Решается проблема рассмотренными выше способами.