Кодирование и обработка в компьютере вещественных чисел

Вернемся к обсуждению того обстоятельства, что в компьютере для записи числа в любой форме представления отводится конечное число разрядов. Для целых чисел это обстоятельство привело к появлению понятий наибольшего целого числа. Однако для каждого целого числа, не превышающего по модулю наибольшего, имеется ровно одно представление в машинном коде и, если не происходит переполнения, результат выполнения операции над целыми числами будет точным, поскольку дискретные множества исходных чисел однозначно отображаются на дискретное множество результатов.

Ситуация радикальным образом меняется при представлении и обработке вещественных чисел. На математической числовой оси вещественные числа образуют непрерывное множество (континуум), т.е. два числа могут находиться сколь угодно близко друг к другу, и на любом отрезке содержится бесконечно много значений чисел. В машинном представлении количество возможных значений чисел конечно; для двоичной системы счисления оно определяется как %%2^k%%, где %%k%% - количество двоичных разрядов в представлении мантиссы. Т.е. вещественные числа в компьютере заменяются их кодами, которые образуют конечное дискретное множество; каждый код оказывается представителем целого интервала значений континуума.

Из данного обстоятельства вытекают ряд следствий:

Следствие 1 состоит в том, что строгие отношения между числами континуума превращаются в нестрогие для их компьютерных представителей, т.е.

• Если %%x^{(1)}>x^{(2)}%%, то %%X^{(1)}\geqslant X^{(2)}%%
• Если %%x^{(1)}=x^{(2)}%%, то %%X^{(1)}= X^{(2)}%%
• Если %%x^{(1)}<x^{(2)}%%, то %%X^{(1)}\leqslant X^{(2)}%%

Следствие 2. Поскольку код вещественного числа в компьютере является приблизительным представителем многих чисел из интервала, то и результаты вычислений также будут заведомо неточными, содержащими неизбежную погрешность. В этом состоит главная особенность обработки вещественных чисел в компьютере - она всегда ведется с погрешностью (кстати, оценка этой погрешности - самостоятельная и непростая задача).

Следствие 3. Наряду с понятием наибольшего вещественного числа (из-за ограниченности разрядной сетки) появляется понятие наименьшего числа или машинного нуля. Например, в типе Real любое десятичное число, по модулю меньшее 2,3∙10-39 оказывается машинным нулем, т.е. считается равным 0 при сохранении и в операциях с ним. Таким образом, математическое понятие «0» как точное значение числа в компьютерном представлении заменяется понятием «машинный нуль» как значение числа меньшее некоторой определенной величины.

Как уже было сказано, основной формой представления кодов вещественных чисел в компьютере является двоичная нормализованная. При этом записываться и храниться в памяти компьютера должны все составляющие нормализованной формы (знак числа, мантисса, знак порядка и порядок), что требует нескольких ячеек памяти. Например, числа типа Real («вещественный») из языка java размещаются в 6 байтах, т.е. 48 двоичных разрядах. Непосредственное распределение компонентов нормализованного числа по разрядам определяется конструктивными особенностями компьютера и программным обеспечением. Ниже приведен пример размещения числа в двух ячейках памяти (32 разряда):

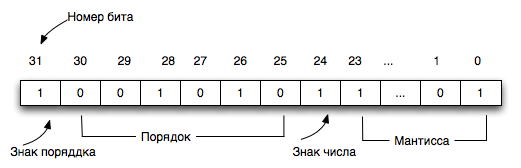
Поскольку значение мантиссы лежит в интервале %%0,12 ≤ М_2 < 1%%, ноль в разряде целых и разделитель десятичных разрядов в представление не включается, т.е. мантисса содержит только цифры дробной части. Более того, можно не сохранять и первую значащую цифру мантиссы, поскольку она всегда 1 (но, естественно, восстанавливать ее при вычислениях) - это дает возможность хранить дополнительный «скрытый» разряд, т.е. несколько повысить точность обработки. В ходе выполнения арифметических операций, как указывалось ранее, производится нормализация промежуточных и конечного значений, состоящая в сдвиге мантиссы вправо или влево с одновременным изменением порядка, что эквивалентно смещению разделителя десятичных разрядов - именно по этой причине такая форма представления числа получила название «с плавающей запятой». Как и в случае целых чисел, для кодов вещественных чисел существует понятие переполнение, однако возникает оно не после заполнения разрядной сетки мантиссы - это приводит лишь к нормализации числа, а при заполнении всех разрядов порядка. Для представленного выше примера размещения числа в 32-х битах, очевидно,

%%|x_2|^{max}=0,111111 111111 111111 111111_2 \cdot 2^{11111} \approx 2.147_{10}\cdot 10^9%%

При этом точность обработки составит 7 десятичных разрядов. При %%|Х_2| > |X_2|^{max}%% возникнет переполнение, т.е. операция станет некорректной.

Пример. Установить распределение разрядов двоичного представления числа типа Real, если для его записи отводится 48 бит, а максимальное значение десятичного порядка 38. Какова точность обработки таких чисел?

• 2 бита расходуется на запись знака числа и порядка;
• %%k_2 = 3.322\cdot k_{10}%%; поскольку %%k_{10} = 38%%, очевидно, максимальный показатель порядка двоичного числа %%k_2 = 3.322 \cdot 38 = 126_{10}%%, что требует в двоичном представлении, согласно формуле Хартли, 7 бит;
• под запись мантиссы отводится %%48 - 2 - 7 = 39%% бит;
• с учетом скрытого разряда точность обработки составит %%(39 + 1)/3,322 ≈ 12%% десятичных разрядов.

Изначальной причиной возникновения погрешности обработки кодов вещественных чисел является ограниченность разрядной сетки при их представлении и, следовательно, наличие погрешности неизбежно. Однако ее величина зависит от количества имеющихся разрядов и, в частности, уменьшить погрешность можно за счет расширения разрядной сетки, т.е. выделения большего количества ячеек памяти для записи числа.

Несколько вариантов представления вещественных чисел в языках программирования высокого уровня используется как одно из средств оптимизации программы. Повышение точности вычислений требует больших ресурсов памяти компьютера; одновременно с этим возрастает и время вычислений. Таким образом, при составлении программы для практической задачи решается проблема нахождения компромисса между точностью результата и временем обработки.

В процессе выполнения арифметических действий с нормализованными числами отдельно обрабатываются мантиссы и порядки. Поскольку операции над кодами вещественных чисел в компьютере обладают некоторой спецификой по сравнению с обычными арифметическими, будем обозначать их следующим образом: %%⊕%% - сложение (вычитание), %%⊗%% - умножение, %%Ø%% - деление.

Сложение нормализованных чисел.

Пусть имеются два числа %%Х_1 = М_1 \cdot p^{k_1}%% и %%Х_2 = М_2 \cdot р^{k_2}%% (здесь индексы у мантиссы и порядка означают не систему счисления, а служат номерами чисел). Сложение должно начинаться с выявления большего из %%k_1%% и %%k_2%%, нахождения модуля их разности %%∆k = |k_1 – k_2|%% и сдвига вправо на %%∆k%% разрядов мантиссы того числа, у которого k оказался меньше. После этого выполняется сложение мантисс, порядку результата присваивается значение большего из имеющихся и при необходимости производится нормализация результата. Алгоритм сложения нормализованных чисел представлен в виде блок-схемы на рисунке ниже. При сдвиге вправо мантиссы меньшего числа происходит потеря %%∆k%% младших значащих цифр, что приводит к появлению погрешности сложения.

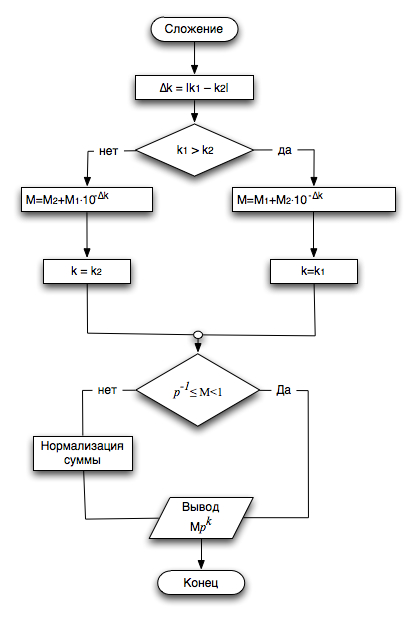
Рассмотрим действие алгоритма на примере сложения десятичных чисел в ограниченной разрядной сетке.

Пример. Найти сумму %%X_1 = 0,87654\cdot 10^1%%, а %%Х_2 = 0,94567 \cdot 10^2%%, если для записи мантиссы отводится 5 разрядов.

Согласно алгоритму %%∆k = 1%% и %%k_1 < k_2%%. Следовательно, %%k = k_2 = 2%%, а мантисса числа %%X_1%% должна быть сдвинута на 1 разряд вправо (при этом из-за ограниченности разрядной сетки пропадет цифра 4). Новая мантисса получается суммированием %%М = 0,94567 + 0,08765 = 1,03332%%; поскольку она выходит за допустимый интервал представления мантисс, необходимо его нормализовать %%М' = 0,10333%% (при этом теряется цифра 2 в младшем разряде); %%k' = k + 1 = 3%%. Окончательно получаем: %%X = - 0,10333 \cdot 10^3%%. Точный результат суммирования оказался бы 103,3324.

Следствием существования погрешности сложения (и, в равной мере, вычитания) кодов вещественных чисел оказывается то, что такое суммирование не обладает ассоциативностью, т.е. в общем случае

%%(x_1\oplus x_2)\oplus x_3 \not = x_1\oplus (x_2\oplus x_3) %%

Вычитание нормализованных чисел, как и чисел целых, не является самостоятельной операцией и сводится к сложению с дополнительным кодом числа.

Умножение нормализованных чисел %%Х_1⊗Х_2%% производится в соответствии с правилами: если по-прежнему %%X_1 = M_1 \cdot р^{k_1}%% и %%Х_2 = m_2 \cdot p^{k_2}%%, то, очевидно, мантисса произведения %%m = m_1 \cdot m_2%%, а порядок %%k = k_1 + k_2%%; при необходимости полученное число нормализуется.

Операция деления, проводимая как над целыми, так и вещественными числами, приводит в общем случае к появлению вещественного числа, поэтому целые числа предварительно преобразуются в вещественный тип, т.е. переводятся в нормализованную форму. Очевидно, при делении %%Х_1∅Х_2%% мантисса частного %%m = \frac{М_1}{М_2}%%, а порядок %%k = k_1 - k_2%%. При этом непосредственно операция деления сводится к сдвигу делителя вправо и последовательному вычитанию его из делителя (т.е. сложения с дополнительным кодом вычитаемого). Как и в предыдущих операциях, результат деления при необходимости нормализуется.

В операциях умножения нормализованных чисел в компьютере возможны ситуации, когда не будут в точности выполняться сочетательный и распределительный законы, т.е.

%%(x_1\oplus x_2)\oplus x_3 \not = x_1\oplus (x_2\oplus x_3) %% и %%(x_1\oplus x_2)\oplus x_3 \not = x_1\oplus x_2\oplus x_3 %%

Время выполнения операций с кодами вещественных чисел в форме с плавающей запятой гораздо больше, нежели с числами целыми или с фиксированной запятой. По этой причине для ускорения обработки на компьютерах IBM с процессорами Intel 80286 и 80386 ставились так называемые «математические сопроцессоры»; в современных компьютерах команды (точнее, микропрограммы, поскольку они содержат последовательность действий) обработки вещественных чисел включены в перечень команд центрального процессора.

Заканчивая рассмотрение порядка обработки чисел в компьютере, хотелось бы сделать ряд общих замечаний:

1. В компьютерах арифметические устройства выполняют действия не с самими двоичными числами по правилам двоичной арифметики, а с их двоичными кодами (представлениями) по правилам арифметики двоичных кодов.
2. Причиной отличий правил арифметики двоичных кодов от правил обычной арифметики является ограниченность разрядной сетки, применяемой для записи чисел в компьютере. По этой же причине отличаются понятия «ноль» и «машинный ноль», «бесконечность» - «максимальное число», а также становится возможной ситуация переполнения, что требует ее постоянного отслеживания.
3. Применение при вычислениях формы представления чисел с плавающей запятой обеспечивает единообразие при их записи и обработке, и, что важно, в результате автоматического масштабирования числа на каждом этапе его обработки сокращается погрешность вычислений.
4. Различие правил обработки целых и нормализованных чисел приводит к необходимости точного описания типов переменных перед их использованием в программах. Вторая причина описания типов состоит в оптимизации расходования памяти компьютера, поскольку числа разных типов требуют для хранения различных ресурсов памяти.