Планарные графы. Раскраски

Исторически планарные графы связаны с одной знаменитой задачей.

Задача о домиках и колодцах. В некоторой деревне есть три колодца. Трое жителей, живущие в трех стоящих рядом домиках перессорились, и решили так протоптать тропинки от своих домов к каждому из трех колодцев, чтобы они не пересекались. Удастся ли им выполнить свой план?

Рисунок 8. Домики и колодцы

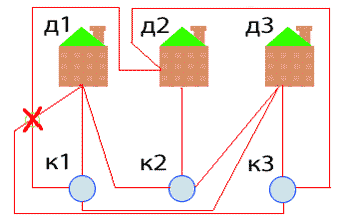
Попробуем решить эту задачу. Проведем тропинки так, как это показано на рисунке 8. Как видно, нам удалось провести только восемь тропинок, а девятая должна пересечься хотя бы с одной. Можно доказать (мы не будем приводить строгое доказательство), что эта задача не имеет решения. Дело в том, что по мере проведения тропинок из двух первых домиков, будет получаться некоторый замкнутый контур, внутри которого будет стоять один из колодцев, при этом третий домик будет находиться снаружи от этого контура. Для того чтобы соединить этот домик с колодцем, обязательно потребуется пересечь новой тропинкой одну из уже проложенных.

Можно предложить еще одну задачу.

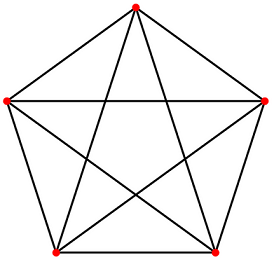
Задача о пяти хуторах. Пять хуторов расположены в вершинах правильного пятиугольника. Нужно проложить дороги от каждого из них к остальным так, чтобы не было перекрестков.

Эта задача также не может быть решена.

• 
• 

Рисунок 9. Графы к задачам о домиках и колодцах и о пяти хуторах

На рисунке 9 построены графы %%K_{3,3}%% и %%K_5%% , соответствующие задаче о домиках и колодцах и задаче о пяти хуторах. Оказывается, что проблема укладки графа на плоскости тесно связана с этими типами графов.

Перейдем теперь к более строгим формулировкам.

Определение 7. Граф называется планарным, если его можно изобразить на плоскости без самопересечений. Такое изображение называют плоской укладкой графа.

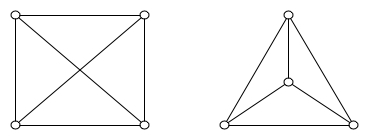
На рисунке 10 изображен полный граф и его плоская укладка.

Рисунок 10. Граф и его плоская укладка

Далее нам понадобится понятие гомеоморфизма. Это очень сложное математическое понятие, но в отношении к графам оно формулируется довольно просто. Мы не будем давать строго определения, а рассмотрим это свойство на примерах.

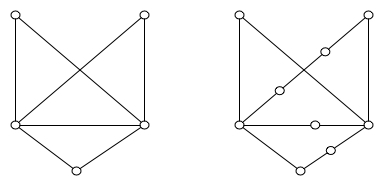
Будем говорить, что два графа гомеоморфны, если один из них получен из другого, путем добавления новых вершин на уже имеющиеся ребра.

На рисунке 11 показаны два гомеоморфных графа. Граф справа получен из первого графа добавлением четырех вершин. На практике бывает довольно трудно увидеть, что два графа гомеоморфны.

Рисунок 11. Гомеоморфные графы

Теперь сформулируем условие планарности графов.

Теорема 8. Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных %%K_{3,3}%% и %%K_5%%.

Эта общая теорема ставит окончательную точку в рассмотренных выше задачах о хуторах и о домиках и колодцах.

Замечание. Доказать что граф планарен и построить его плоскую укладку – это две независимых задачи. Заметим, что если граф не имеет пяти вершин, степень которых не меньше четырех, то он наверняка не имеет подграфа, гомеоморфного %%K_5%%. Если в графе нет шести вершин, степень которых не меньше трех, то он гарантированно не имеет подграфа, гомеоморфного %%K_{3,3}%%. Однако построить плоскую укладку графа с достаточно большим количеством вершин бывает непросто.

Рассмотрим теперь еще одну классическую задачу теории графов.

Задача о четырех красках. На политической карте мира нарисовано несколько государств. Карту нужно раскрасить так, что бы две страны, имеющие общую границу, были покрашены в разные цвета.

В классическом варианте предполагалось, что карту можно раскрасить четырьмя цветами. Покажем, как эта задача связана с графами. Обозначим каждую страну на карте точкой, вершины, отвечающие странам, имеющим общую границу, соединим ребрами. Теперь задачу о раскрашивании можно сформулировать так: раскрасить вершины планарного графа так, чтобы любые две смежные были покрашены в разные цвета. Эта задача может быть решена для графов с малым количеством вершин. Если же число вершин достаточно велико, то гипотеза четырех красок оказывается неверной. (Этот факт установлен с помощью мощных компьютеров.) Вместе с тем, довольно простыми средствами была доказана теорема о пяти красках.

Теорема 9. Планарный граф можно раскрасить пятью красками так, что любые смежные вершины будут окрашены в разные цвета.

Еще одна интересная проблема: сколькими способами можно раскрасить граф, если имеется %%n%% красок.

Оказывается, что число способов раскрашивания является многочленом от %%n%%, коэффициенты этого многочлена можно вычислить с помощью специального алгоритма.

Укажем еще одно обобщение задачи о раскрасках. Известно, что граф без самопересечений располагается на некоторой поверхности (на сфере, на торе, на бутылке Клейна и т.п.), какое минимальное количество красок нужно для его раскрашивания?

Ответ на этот вопрос был получен в разделе математики, называющемся «топологией». Оказалось, что для всех замкнутых двумерных поверхностей (кроме сферы), данное число выражается через Эйлерову характеристику этой поверхности.