Что такое граф?

На рисунке 1 показан пример графа.

Рисунок 1. Граф с семью вершинами

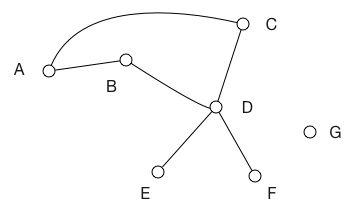
Как вы видите, ребрами соединены не все вершины графа. Вершины, из которых не выходит ни одного ребра, называют изолированными. (На рисунке изолированная вершина это точка G). С помощью графов удобно и наглядно изображается информация о разных объектах и отношениях между ними. Рассмотрим пример.

Пример 1. В розыгрыше финальной части турнира участвуют семь команд: шесть команд, набравших наибольшее количество очков в предварительной части турнира и команда – победитель прошлого года. Сначала играют друг с другом первые шесть команд, затем три команды, одержавшие победы и команда, победитель прошлого года, играют друг с другом. Два победителя этого тура встречаются в финале.

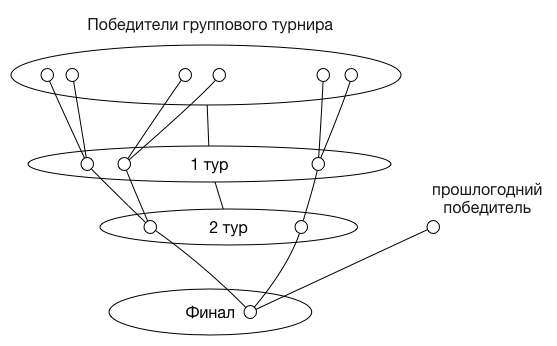
Понять о чем идет речь в этом тексте нелегко. Попробуем представить его в виде наглядной схемы (смотри рисунок 2) и порядок организации финальной части розыгрыша станет очевидным.

Рисунок 2. Граф к примеру 1

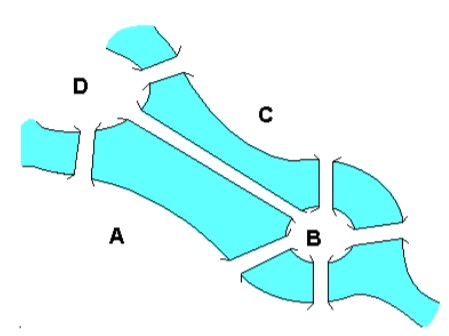
Обратимся теперь к истории появления графов. Впервые в рассмотрение их ввел великий математик Леонард Эйлер. В популярной литературе часто упоминается его задача о Кенигсбергских мостах. Смысл задачи таков: в городе Кенигсберге (ныне это город Калининград) протекает река Прегель. Сам город расположен на берегах этой реки и ее островах. Естественно, что в городе построены мосты, связывающие все его районы (смотри рисунок 3). Во время прогулки по городу Эйлер захотел пройти по всем мостам, но ему это не удалось. Вернувшись домой, ученый составил схему, изобразив участки суши точками, а мосты отрезками (рисунок 4). Это и был первый граф.

Мы ответим на вопрос, можно ли осуществить пешую прогулку по указанному правилу, немного позже, а сейчас рассмотрим некоторые важные свойства графов.

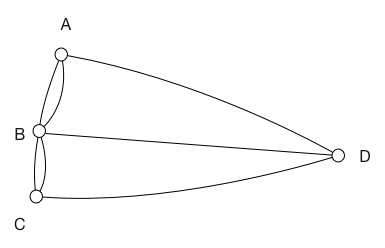
Определение 1. Степенью вершины графа называется число выходящих из него ребер. Степени вершин %%A, C%% и %%D%% на рисунке 4 равны трем, а степень вершины %%B%% равна 5. В графе на рисунке 1 степень вершины %%G%% равна нулю, так как из нее не выходит ни одно ребро. Для степени вершины принято следующее обозначение: %%deg(A)%%. Рассмотрим некоторый граф %%G%%. Обозначим количество его вершин буквой %%p%%, а количество ребер буквой %%q%%.

Сформулируем в виде теорем простейшие свойства степени.

Рисунок 3. Схема мостов в Кенигсберге

Теорема 1. Сумма степеней всех вершин графа %%G%% равна удвоенному количеству его ребер (%%2q%%).

Граф называют простым, если две вершины соединяет не более одного ребра, в противном случае, граф называют мультиграфом. На рисунке 1 изображен простой граф, а на рисунке 4 мультиграф.

Рисунок 4. Граф к рисунку 3

Теорема 2. В простом графе найдется не менее двух вершин с одинаковыми степенями.

Теорема 3. В простом графе с %%p%% вершинами число ребер не больше %% \frac {p(p-1)}{2}%%: $$ \frac {p(p-1)}{2}\geqslant q$$

Доказательство. Всего %%p%% вершин, каждая из них может быть соединена не более чем с %%(p-1)%% остальными вершинами. Таким образом, получаем %%(p-1)p%% ребер, но каждое из них посчитано ровно два раза, так как соединяет две вершины. Поэтому делим полученное выражение пополам.

Определение 2. Граф называется полным, если каждая его вершина соединена со всеми другими вершинами графа.

Примеры полных графов вы можете построить сами: нарисуйте выпуклый многоугольник и постройте все его диагонали. Из доказательства теоремы 2 вытекает, что в полном графе с %%p%% вершинами %% \frac {p(p-1)}{2}%% ребер.