Пути, циклы, связность
Еще одно важное понятие, относящееся к графам – связность. Для того чтобы ввести его, дадим несколько определений. Начнем с понятия путь.
Определение 3. Путем (из вершины А в вершину В) в графе называется последовательная цепочка смежных ребер, которая начинается в вершине А и заканчивается в вершине В. Путь может проходить через ребро только один раз.
(Запись пути в графе зависит от того, как определены его ребра. Если ребра определены с помощью вершин, то записывают последовательность тех вершин, через которые проходит путь. Если же ребра имеют собственные названия, то выписывается последовательность из этих названий.)
Рассмотрим примеры. На рисунке 5 жирными линиями показан путь из точки %%A%% в точку %%B%%, который мы можем записать так: (AEDB). Другой путь из %%A%% в %%B%% показан пунктирными линиями, его можно записать как %%(l_1l_2l_3)%%.
Заметим, что может существовать несколько путей из одной точки в другую. В качестве устного упражнения сосчитайте, сколько всего путей можно указать из вершины А в вершину В. Рассмотрим теперь специфический случай, когда начало и конец пути совпадают.
Определение 4. Циклом называется путь, у которого начало и конец совпадают.
На рисунке 5 циклами являются следующие пути: (AEFDA), (EFBCADE).
Рисунок 5. Пути в графе
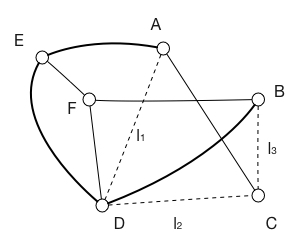
Пути и циклы будем называть простыми, если через каждую свою вершину они проходят только один раз.
Все приведенные в примерах пути и циклы являются простыми.
Определение 5. Граф называется связным, если любые две его вершины можно соединить хотя бы одним путем. В противном случае граф называется несвязным.
Граф на рисунке 1 несвязен, так как нет ни одного пути, соединяющего точку G с остальными вершинами, графы на рисунках 2, 4, 5 - связные.
Вам уже, наверное, приходилось встречать задачи, в которых предлагается обвести ту или иную фигуру, не отрывая карандаш от бумаги. При этом запрещается проводить карандаш по одной линии несколько раз. Понятно, что аналогичное задание может быть дано и относительно некоторого графа. Далеко не все графы можно построить описанным выше способом. Те, для которых это требование выполняется, называются уникурсальными или эйлеровыми. Эти графы непосредственно связаны с задачей о Кенигсбергских мостах и впервые описаны Леонардом Эйлером. Сам Эйлер доказал следующую теорему.
Теорема 4 (Эйлера). Связный граф уникурсален тогда и только тогда, когда степени всех его вершин четны или у него ровно две вершины нечетной степени.
Доказательство. Вначале заметим, что если все вершины графа имеют степень не меньше двух, то в нем существует хотя бы один цикл.
Рассмотрим случай, когда все вершины четны. Применим «метод стирания». Выберем некоторую точку и начнем строить путь. Так как степени всех вершин четны, то они не меньше двух. Поэтому, войдя по некоторому ребру в данную точку, мы всегда можем выйти из нее по второму ребру. Будем отмечать пройденные вершины. Так как число вершин конечно, то на каком то шаге мы перейдем в одну из уже отмеченных вершин и таким образом замкнем цикл. Теперь сотрем этот цикл (естественно, запомнив его где-то) и рассмотрим получившийся граф. Он может оказаться несвязным, но, тем не менее, все его вершины будут иметь четную степень. Применим к этому графу ту же процедуру, и будем это делать до тех пор, пока остается хотя бы один нетривиальный подграф. В результате мы получим несколько циклов, которые не имеют общих ребер, а все вместе образуют исходный граф. Нам остается только склеить эти циклы в один. Возьмем два цикла %%(…ВАС…)%% и %%(…НАМ…)%%, имеющие общую вершину %%А%%, разрежем их в этой вершине и склеим по такому правилу: сначала выписываем вершины первого цикла, потом, дойдя до точки %%А%%, записываем все вершины второго цикла, а затем продолжаем выписывать оставшиеся вершины первого цикла. Очевидно, что в итоге у нас получится один цикл, который содержит все ребра исходного графа.
Предположим теперь, что в исходном графе ровно две нечетных вершины %%A%% и %%B%%. Соединим их дополнительных ребром %%АВ%%, и получим граф, все вершины которого четны. Построим для него эйлеров цикл по указанному выше алгоритму. Перепишем его так, чтобы вершина %%А%% была начальной, а ребро %%АВ%% – последним. Удалив из этого цикла ребро %%АВ%% получим цикл, начинающийся в %%А%% и заканчивающийся в %%В%%. Этот путь проходит через все ребра исходного графа.
Предположим теперь, что граф уникурсален. Докажем, что в нем не более двух нечетных вершин. Очевидно, что рисовать такой граф нужно, начиная с нечетной вершины. Причем завершить маршрут нужно в другой нечетной вершине. Если же имеется еще одна нечетная вершина, то она не может быть ни начальной, ни конечной. Поэтому, когда мы в нее заходим, то должны обязательно выйти. Каждый проход через вершину уменьшает число не пройденных ребер, связанных с этой вершиной, ровно на два. В итоге, на каком то шаге в нечетной вершине останется только одно не пройденное ребро, зайдя по которому в вершину мы уже не сможем из нее выйти. Теорема доказана полностью.
Используя доказанную теорему, убедитесь в том, что задача о Кенигсбергских мостах не имеет решения.
*В более сложной формулировке этой задачи требуется найти наиболее короткий маршрут
Существует еще одна очень интересная задача, связанная с графами. В ней требуется отыскать простой цикл, который проходит через все вершины данного связного графа. Эта задача является частным случаем «задачи коммивояжера*», суть которой в следующем. Коммивояжер (разъездной торговец) должен проехать по всем городам некоторого региона и вернуться в исходный пункт. При этом целесообразно так составить маршрут, чтобы в каждом городе побывать ровно один раз (иначе покупатели могут предъявить счет за некачественный товар). У коммерсанта естественно, имеется карта дорог региона.
Циклы, обладающие указанным выше свойством, называют гамильтоновыми, в честь изобретателя Гамильтона, придумавшего игру – головоломку, в которой требовалось отыскать такие пути.
В отличие от эйлеровых циклов, для гамильтоновых циклов нет исчерпывающего условия, подобного теореме 4.
Имеется следующий достаточный признак.
Теорема 5. Пусть связный граф имеет не меньше четырех вершин %%(p>3)%% и степень каждой вершины не меньше %%\frac{p}{2}%%, тогда в графе имеется гамильтонов цикл.
Рассмотрим граф на рисунке 5. У него 6 вершин, при этом пять вершин имеют степень три, и одна степень пять. Согласно теореме, в этом графе существует гамильтонов цикл. Нетрудно проверить, что таким циклом является цикл (AEFDBCA).
Рассмотрим теперь какой-нибудь выпуклый многоугольник. Его вершины будем считать вершинами, а стороны – ребрами, некоторого графа. Степень каждой вершины такого графа равна двум, и для него, очевидно, не выполняются требования теоремы 5. Но, тем не менее, этот граф является гамильтоновым.
| Что такое граф? | Деревья |