Декартово произведение множеств
В 1637 году вышел философский трактат “Рассуждение о методе” французского философа и математика Рене Декарта (1596—1650). Последняя часть этой работы была посвящена новому геометрическому методу — методу координат. Каждой точке плоскости Декарт поставил в соответствие упорядоченную пару вещественных чисел — ее первую и вторую координаты. При этом многие геометрические фигуры стали описываться с помощью алгебраических уравнений. Координаты каждой точки данной фигуры удовлетворяли соответствующему уравнению, координаты всех остальных точек плоскости не удовлетворяли этому уравнению. Таким образом, многие геометрические задачи были переведены на алгебраический язык и были решены алгебраическими средствами. Эта часть математики, которая возникла на границе геометрии и алгебры, стала называться аналитической геометрией.
Рассмотренное Декартом множество всех упорядоченных пар вещественных чисел является примером произведения множества на себя. Для определения произведения множеств в общем случае необходимо понятие упорядоченной пары.
Пусть %%A%% и %%B%% — произвольные непустые множества и %%a ∈ A%% , %%b ∈ B%% . Заметим сразу, что множества %%\{a, b\}%% и %%\{b, a\}%% равны между собой и поэтому не дают возможности определить, какой из двух элементов пары является первым, а какой — вторым.
Последнее важно, так как, например, точки с координатами %%(1, 2)%% и %%(2, 1)%% различны, в то время как множества %%\{1,2\}%% и %%\{2,1\}%% совпадают.
Существует несколько определений упорядоченной пары %%(a, b)%% , одно из них принадлежит Н.Винеру и К.Куратовскому.
Определение. Пусть %%a ∈ A%%, %%b ∈ B%% . Упорядоченной парой (%%a, b)%% называется множество %%\{\{a\}, \{a, b\}\}%% , при этом %%a%% называется первым элементом упорядоченной пары, а %%b%% — вторым.
Теорема 1.3.1. %%(a,b)=(c,d)⇔a=c%% и %%b=d%%.
Итак, запись %%(a, b)%% означает, что пара образована двумя элементами %%a%% и %%b%% , причем a является первым элементом этой пары. В предыдущей теореме доказано основное свойство упорядоченных пар: две упорядоченные пары совпадают тогда и только тогда, когда совпадают их первые элементы и вторые элементы также равны между собой. Это, в частности, означает, что %%(a, b) = (b, a)%% только в исключительном случае: когда %%a = b%%.
Определение. Произведением двух множеств %%A%% и %%B%% называют множество %%A × B%% , состоящее из всех упорядоченных пар, первые элементы которых выбираются из %%A%%, вторые — из %%B%% (т.е. %%A×B=\{(a,b):a∈A, b∈B\}%%).
На рис. 3 изображено произведение множеств %%A = \{1, 2, 3\}%% и %%B = \{a, b\}%%.
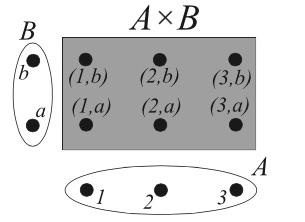
Рис.3
Произведение двух множеств %%A%% и %%B%% часто называют декартовым произведением.
Заметим, что множества %%A%% и %%B%% не обязаны быть различными, в случае их совпадения множество %%A × A%% обозначают через %%A^2%% и называют квадратом (декартовым квадратом) множества %%A%% . Так, например, %%R^2%% — декартова плоскость, %%Z^2%% — ее подмножество, состоящее из всех точек с целочисленными координатами.
Заметим,что часто %%A×B\not=B×A%%. Так, %%(1,−2)∈N×Z%%,но %%(1,−2)\not ∈Z×N%%.
Теорема 1.3.2. Пусть %%A%%, %%B%% и %%C%% — произвольные множества, тогда выполняются следующие свойства:
$$1.(A∪B)×C =(A×C)∪(B×C), $$ $$1′.(A∩B)×C =(A×C)∩(B×C).$$
| Операции над множествами и их свойства | Соответствия |