Операции над множествами и их свойства
Довольно часто новые множества с требуемыми свойствами получаются из ранее построенных с помощью теоретико-множественных операций. Последние имеют своими историческими предшественниками логические операции, свойства которых были хорошо изучены уже к середине XIX века. В этом параграфе изучаются основные теоретико-множественные операции: пересечение, объединение, разность множеств и взятие дополнения.
Определение. Пересечением множеств %%A%% и %%B%% (обозначается %%A ∩ B%% ) называется множество, состоящее из всех элементов, которые одновременно принадлежат и %%A%% , и %%B%% . Символьная запись этого определения такова:
$$A ∩ B = \{x : x ∈ A и x ∈ B\}$$
Определение. Объединением множеств %%A%% и %%B%% (обозначается %%A ∪ B%% ) называется множество, состоящее из всех элементов, принадлежащих или %%A%% , или %%B%% . И соответствующая символьная запись:
$$A∪B = \{x : x ∈ A \text{ или } x ∈ B\} $$
Диаграммы Эйлера–Венна, изобpаженные на рис.1 и 2, являются иллюстрацией для включения множеств, а также операций пеpесечения и объединения.
Рассмотрим несколько примеров. Если %%A = \{1,2,3\}%% и %%B = \{3,4\}%%, то их пересечением будет множество %%A ∩ B = \{3\}%% , а объединением — %%A ∪ B = \{1, 2, 3, 4\}%% . Пересечение множества, состоящего из всех квадратов плоскости, и множества четырехугольников, не являющихся квадратами, пусто, в то время как их объединение дает множество всех четырехугольников на плоскости.
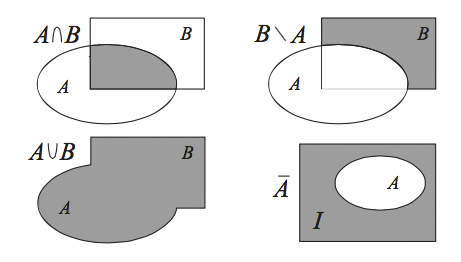
Рис. 2
Решением любой системы уравнений является пересечение решений каждого из входящих в систему уравнений. Пересечение двух различных прямых не может содержать более одной точки, а объединение всегда бесконечно, так как содержит каждую из этих прямых.
Перед тем как определить еще одну операцию над множествами, обсудим понятие универсального множества. Часто рассматривают множества какого-то определенного типа, т.е. все они одновременно содержатся в некотором “большом” множестве. Такое множество, которое содержит все рассматриваемые множества данного типа, называется универсальным для этого типа множеством. Так, для знакомого множества крокодилов моря Лаптевых универсальным %%A%% множеством является множество всех крокодилов.
Для четырехугольников универсальным множеством является плоскость. Для числовых множеств — множество всех вещественных чисел %%\mathbb R%% . Далее универсальное множество будем обозначать через %%I%% .
Определение. Разностью множеств %%B%% и %%A%% (обозначается %%B \backslash A%% ) называется множество, состоящее из всех элементов множества B , не принадлежащих множеству A (т.е. %%B\backslash A=\{x:x∈B \text{ и } x \not ∈ A\}%%) (pис. 2).
Определение. Дополнением множества %%A%% (обозначение — %%\overline{A}%% ) называется разность между универсальным множеством %%I%% и множеством %%A%% (т.е. %%\overline{A} = \{x : x ∈ I\text{ и } x\not ∈ A\}%%) (pис. 2).
Если по-прежнему %%A = {1,2,3}%% и %%B = {3,4}%%, то %%B\backslash A = \{4\}%%, а %%A\backslash B = \{1, 2\}%% . Разностью между множеством натуральных чисел %%\mathbb N%% и множеством всех четных натуральных чисел %%N_2%% является множество всех нечетных натуральных чисел.
Операции объединения и пересечения удовлетворяют следующим свойствам.
Теорема 1.2.1. Пусть %%A%%, %%B%% и %%C%% — произвольные множества. Тогда справедливы следующие равенства:
$$1. A ∪ A = A. $$ $$2. A ∪ B = B ∪ A.$$ $$3. (A∪B)∪C =A∪(B∪C).$$ $$4. (A∪B)∩C =(A∩C)∪(B∩C). $$
$$1′. A ∩ A = A. $$ $$2′. A ∩ B = B ∩ A.$$ $$3′.(A∩B)∩C =A∩(B∩C). $$ $$4′.(A∩B)∪C =(A∪C)∩(B∪C). $$
Свойства 2 и 2′ называются законом коммутативности операций %%∪%% и %%∩%% , 3 и 3′ — законом ассоциативности, 4 и 4′ — дистрибутивности.
Легко заметить, что опеpации %%∪%% и %%∩%% обладают некотоpой симметpичностью. Так, пpи одновpеменной замене всех %%∪%% на %%∩%% и всех %%∩%% на %%∪%% каждая из пpиведенных выше фоpмул останется верной. В следующей теоpеме показываются основные свойства разности множеств.
Теорема 1.2.2. Пусть %%A%% и %%B%% произвольные множества. Тогда выполняются следующие свойства:  $$5. A ∪ \oslash = A.$$ $$6. A ∪ I = I.$$ $$7. \overline{A ∪ B} = \overline{A} ∩ \overline{B}.$$
$$5′. A ∩ \oslash = \oslash.$$ $$6′. A ∩ I = A.$$ $$7′. \overline{A ∩ B} = \overline{A} ∪ \overline{B}.$$ $$8. A = A.$$
Свойства 7 и 7′ называются законами де Моргана.
| Множество и его элементы. Способы задания множеств | Декартово произведение множеств |