Соответствия
Определение. Соответствием φ между множествами %%A%% и %%B%% называется произвольное подмножество их произведения %%A × B%% (т.е. %%φ ⊆ A × B%% ).
Итак, соответствие состоит из упорядоченных пар. Каждая пара %%(a, b) ∈ φ%% указывает, что элементу %%a ∈ A%% соответствует элемент %%b ∈ B%% при данном соответствии %%φ%%.
Иногда соответствие удобно изображать с помощью стрелок, начало которых указывает первый элемент упорядоченных пар, конец — второй элемент. Так, рис. 4 является изображением для следующего соответствия:
%%φ = \{(1, b), (3, a), (3, c), (4, b)\}%%
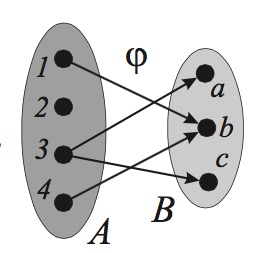
Рис. 4.
Заметим, что некоторым элементам из %%A%% может соответствовать несколько элементов множества %%B%%, а некоторым элементам из %%A%% может не соответствовать ни один элемент множества %%B%% .
Определение. Областью определения соответствия φ называется множество %%Dom\, φ=\{a∈A: \text{ существует элемент } b∈B, \text{ что }(a,b)∈φ\}%% (т.е. это все элементы из %%A%% , которым соответствует хотя бы один элемент из %%B%% ).
Определение. Множеством значений соответствия %%φ%% называют множество %%Im\, φ = \{b ∈ B : \text{ существует элемент }a ∈ A,\text{ что }(a, b) ∈ φ\}%% (т.е. это все элементы из %%B%% , которые соответствуют хотя бы одному элементу из %%A%% ).
Пример 1. Для %%φ%%,изображенного на рис.4, %%Dom\,φ = \{1,3,4\}%% и %%Im\, φ = \{a,b,c\}%%. Для обозначения соответствия %%φ%% между множествами %%A%% и %%B%% будем использовать %%φ:A→B%%.
Опишем некоторые типы соответствий.
Определение. Соответствие %%φ%% называется
- всюду определенным, если %%Dom\, φ = A%% ;
- сюръективным, если %%Im\, φ = B%% ;
- однозначным, если каждому %%a ∈ Dom\, φ%% соответствует единственный элемент %%b%% из %%B%%,т.е. из %%(a,b)∈φ%% и %%(a,b_1)∈φ⇒b=b_1%% ;
- инъективным, если разным элементам из %%Dom\, φ%% соответствуют разные элементы из %%B%%,т.е. из %%(a,b)∈φ%% и %%(a_1,b)∈φ⇒a=a_1%%.
Пример 2. Так, соответствие %%φ%% из примера 1 сюръективно, но не всюду определено ( %%2\not ∈ Dom\,φ%% ), не однозначно (так как %%(3, a), (3, c) ∈ φ%% ), не инъективно (так как %%(1, b), (4, b) ∈ φ%% ). Чаще всего мы будем иметь дело с “хорошими” соответствиями — отображениями и биекциями.
Определение. Отображением называется всюду определенное и однозначное соответствие (выполняются свойства 1 и 3). Функцией называют отображение в вещественную прямую (т.е. %%B = \mathbb R%% ).
Определение. Биекцией называют всюду определенное, сюръективное, однозначное и инъективное соответствие (выполняются все свойства 1—4).
Например, квадратичная функция каждому числу %%x ∈ R%% (поэтому она всюду определена) ставит в соответствие одно число %%ax^2 + bx + c%% (она однозначна). Но квадратичная функция не является инъективным соответствием (некоторым pазличным числам она ставит в соответствие одно и то же число). Поэтому это не биекция. С другой стороны, функция %%f(x) = kx + b%% является биекцией при %%k\not= 0%% .
К соответствиям можно применять две операции — рассматривать обратное соответствие и брать композицию соответствий.
Определение. Обратным соответствием к соответствию %%φ ⊆ A × B%% называют %%φ^{−1}%% %% = \{(b,a) : (a,b) ∈ φ\}%%.
Заметим, что %%φ^{−1}%% %% ⊆ B × A %%, поэтому %%φ^{−1}%% — это соответствие уже между %%B%% и %%A%% . На рис. 5 показано обратное соответствие к φ , изображенному на рис. 4. В этом случае %%φ^{−1}%% %% = \{(b, 1), (a, 3), (c, 3), (b, 4)\} %%.
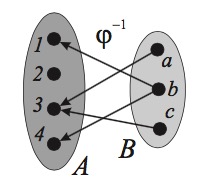
Рис. 5
Определение. Композицией соответствий %%φ ⊆ A×B и ψ ⊆ B×C%% называют соответствие %%χ ⊆ A × C%% такое, что %%χ = \{(a, c) : \text{ существует элемент } b ∈ B,\text{ что }(a,b)∈φ\text{ и }(b,c)∈ψ\}%% (обозначается композиция так: %%χ=ψ◦φ%%).
Композиция соответствий, изображенных на рис. 6, является множеством %%ψ◦φ=\{(1,y), (3,x), (4,y)\}%%.
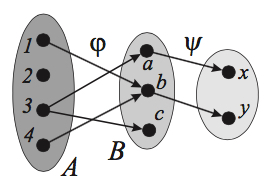
Рис. 6
| Декартово произведение множеств | Примеры решения задач |