Множество и его элементы. Способы задания множеств
Во многих математических теориях существуют первоначальные, или неопределяемые, понятия.
Причина, по которой невозможно определить абсолютно все понятия, которые мы используем, состоит в следующем. Определяя некоторое понятие через другие, необходимо следить за тем, чтобы это понятие не было определено само через себя. Иначе может возникнуть определение, которое в математике называется “порочным кругом” и считается недопустимым. Вот несколько примеров таких “определений”: “ромб — это ромб”, “угол имеет величину %%90^\circ%% , если его стороны перпендикулярны; перпендикулярными прямыми называются прямые, угол между которыми %%90^\circ%% ” и т.д.
Каждое определение в математике — это замаскированная цепочка определений, каждое звено которой является переходом к определению более простого понятия. Поскольку замыкать цепь нельзя, то каждый нижний уровень цепи является неопределяемым понятием.
Так, давая строгое определение ромба, можно через определение замкнутой простой ломаной и ее звена дойти до двух не определяемых в геометрии понятий — точки и прямой. От первоначальных понятий требуется очень многое: при небольшом количестве они должны обеспечить все многообразие понятий данной математической теории. Все необходимые для этого свойства неопределяемых понятий описываются с помощью системы аксиом.
Аксиомы — это утверждения о неопределяемых понятиях, которые мы заранее (т.е. по определению) считаем истинными.
Так, по Гильберту, в геометрии существуют три неопределяемых понятия, которые описываются двадцатью аксиомами.
Единственным неопределяемым понятием в теории множеств является понятие множества. В качестве синонимов множеству мы будем использовать “совокупность элементов” или “класс элементов”. Смысл множества интуитивно ясен — множество объединяет некоторые, вполне определенные, элементы в одно целое. Трудно найти объекты, которые не являются множествами. Так, эта страница является множеством, состоящим из строк, каждая строка — множество, состоящее из некоторых символов, каждый символ — множество точек на плоскости.
Множества мы будем обозначать большими буквами %%( A , B , X , Y )%%, его элементы — малыми %%( a, b, x, y )%%. Тот факт, что a является элементом множества %%A%% , будем обозначать %%a ∈ A%% (читается: a принадлежит множеству A ). Знак %%∈%% был введен итальянским математиком Дж.Пеано и является сокращением греческого слова εστι — “быть”. Запись %%a\not\in A%% означает, что a не является элементом множества %%A%% .
Множество полностью определяется своими элементами. Это означает, что множества совпадают в том и только в том случае, когда они состоят из одних и тех же элементов. Символьная запись определения равенства двух множеств такова:
$$A=B ⇐⇒ (\text{для любого } a∈A⇒a∈B \text{ и для любого } b ∈ B ⇒ b ∈ A ).$$
Существует два основных способа задания множеств. Для конечных множеств, содержащих небольшое количество элементов, часто просто перечисляют все входящие в него элементы. Так, например, %%A = {a,b,c}%% — это множество, элементами которого являются только %%a%%, %%b%% и %%c%% .
Самым распространенным является задание множества с помощью некоторого условия %%P(a)%%, которому удовлетворяют все элементы этого множества и только они.
Иными словами, условие %%P(a)%% истинно во всех случаях, когда элемент %%a%% должен принадлежать определяемому множеству, и ложно для всех элементов, не участвующих в образовании этого множества. Запись %%A = \{a : P(a)\}%% означает, что множество %%A%% состоит из всех элементов, которые удовлетворяют условию %%P(a)%% (знак “:” означает “такие, что” ).
Например,
$$N_2 = \{n : n ∈ N \text{и существует некоторое } k ∈ N, \text{ что } n = 2k\}$$ множество всех четных натуральных чисел;
множество $$R^+ = \{x : x ∈ R \text{ и } x \geqslant 0\}$$ состоит из всех неотрицательных вещественных чисел,
$$B = \{b : b \text{ является выпуклым четырехугольником}\}$$ множество, состоящее из всех выпуклых четырехугольников, или такое экзотичное множество, как
$$Y = \{y : y \text{ -- крокодил, обитающий в море Лаптевых }\}$$
Для сокращения записи вместо %%A = \{a : a ∈ B и P (a)\}%% будем использовать запись %%A = \{a ∈ B : P (a)\}%% .
Множества могут являться частью других множеств. Так, множество натуральных чисел %%N%% содержится во множестве всех целых чисел %%Z%% , последнее — во множестве рациональных чисел %%Q%% , и, наконец, множество %%Q%% содержится во множестве вещественных чисел %%R%% .
Определение. Множество %%A%% содержится во множестве %%B%% (обозначается %%A ⊆ B%% ), если каждый элемент множества %%A%% является элементом множества %%B%% (рис. 1).
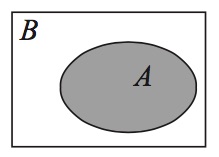
Рис. 1
Теорема 1.1.1. %%A = B%% тогда и только тогда,когда одновременно %%A⊆B%% и %%B⊆A%% (т.е. %%A= B ⇐⇒ A ⊆ B \text{ и } B ⊆ A%% ).
Бывают случаи, когда условие %%P(a)%% определено таким образом, что нет ни одного элемента, который бы удовлетворял этому условию. Например, %%P (a) = a%%, где %%a%% является четным и одновременно нечетным натуральным числом.
Множество, не содержащее ни одного элемента, обозначается %%\oslash%% и называется пустым множеством.
Его можно определить еще и таким образом:
$$\oslash = {x : x — множество \,и\, x\not = x}$$
Важное замечание о пустом множестве.
Предположим, необходимо доказать, что каждый элемент %%x%% данного множества %%A%% удовлетворяет некоторому свойству %%P ′(x)%% . В случае, когда множество %%A%% не содержит элементов, т.е. является пустым, пpинято считать, что каждый его элемент удовлетворяет свойству %%P ′(x)%% .
| Основы теории множеств | Операции над множествами и их свойства |