Примеры решения задач

Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?

Решение. Обозначим через %%А%% — множество школьников, знающих английский язык; %%N%% — множество школьников, знающих немецкий язык; %%F%% — множество школьников, знающих французский язык.

Тогда

$$n(A) = 42, n(N) = 30, $$ $$n(F) = 28, $$ $$n(A ∩ N) = 5,$$ $$n(A ∩ F) = 10, $$ $$n(N ∩ F) = 8, $$ $$n(A ∩ N ∩ F) = 3$$

Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.

$$n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =$$ $$= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =$$ $$= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.$$ Следовательно, не знают ни одного иностранного языка: %%100 – 80 = 20%% школьников.

Эту же задачу можно решить с помощью диаграммы Эйлера–Венна (рис. 1).

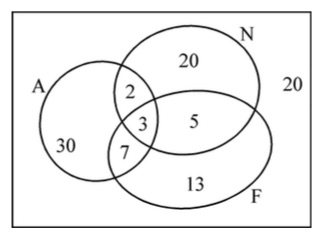
Так как 3 языка знают 3 школьника, то английский и немецкий знают %%5 – 3 = 2%%, английский и французский — %%10–3=7%%, немецкий и французский — %%8 – 3 = 5%% школьников. Только английский знают %%42 – (2+3+7)=30%%, только немецкий — %%30–(2+3+5)=20%%, только французский — %%28 – (3 + 5 + 7) = 13%% школьников. Ни одного языка не знают %%100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20%% школьников.